Why the Dice Are More Important in Craps than the Table

If you’ve been to the casino and watched a craps game in action, you’d be forgiven for overestimating the important of the craps table to the game. After all, it’s huge, and you have multiple dealers overseeing the action there. The dice are just these 2 small cubes that the players are throwing around.

Also, look at the table. It’s full of lines and numbers and words. I don’t even know what half the bets on the craps table mean, and I write about craps (and other kinds of gambling) for a living.
The reality is that, at its core, craps is a simple game. The dice are the most important factor in the game, too.

This post explains why:

Understanding the Probabilities behind the Dice

Before I even start to talk about how to play the game or what kinds of bets are good or bad, let’s look at what the probabilities are when you’re rolling 2 dice.

When you roll 2 dice, you have the following possible totals:

• 2
• 3
• 4
• 5
• 6
• 7

• 8
• 9
• 10
• 11
• 12

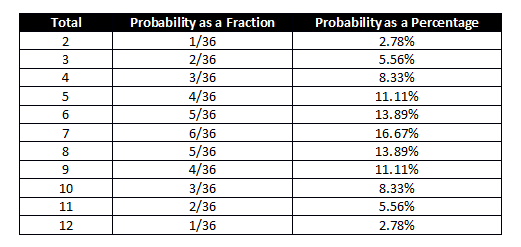
You only have 11 possible totals, but that’s not the total number of possible combinations. That’s because there are multiple ways to generate most of these totals.

Of course, when you’re talking about a 2 or a 12, you only have one way to make each total. You can only get a total of 2 if you wind up with a 1 on the first and on the 2^nd die. You can only get a total of 12 if you get a 6 on the first dice and a 6 on the 2^nd die.

But the number of combinations go up fast after that.

You have 2 different ways of getting a total of 3. You can get a 1 on the first dice and a 2 on the 2^nd die. OR you can get a 2 on the first dice and a 1 on the 2^nd die. (And yes, those do count as 2 different possible combinations.)

The more ways you can generate a total, the likelier it is that you’ll get that total. A total of 7 is the highest probability results, because there are so many ways to wind up with a total of 7:

That’s 6 possible ways to achieve that total.

In fact, you have 36 different ways the dice can turn out.

Understanding this is the beginning of craps wisdom.

Craps and Dice Probability

Probability, in general, is the study of how likely something is to happen or not. It’s a branch of mathematics, and it’s easier to understand than you might think. (It’s definitely easier than calculus or even geometry.)

Probability is mostly about division.

Probability also refers to the likelihood that something will happen. (It’s not just the expression used to discuss that branch of math.)

An event’s probability is always a number between 0 and 1. This means it’s always a fraction, which is also always a division problem. You can express a fraction in multiple ways, too.

Something that will always happen has a probability of 1, but most people would express that as a percentage—100%.

Something that will never happen has a probability of 0, and most people would express that as a percentage, too—0%.

The formula for describing an event’s probability is just the number of ways something can happen divided by the total possible number of events.

Since we know that there are 36 possible results when you roll 2 dice, the probabilities always involve dividing by 36.

The probability of rolling a 2, for example, is 1/36, or 2.78%. You only have one combination that will generate a 2 out of 36 possible combinations.

The probability of rolling a 3 is 2/36, which can be reduced to 1/18, which is also the same thing as 5.56%.

You can continue to do this with all the totals:

Now that we know those probabilities, we can look at one other way to express a probability in craps or any other gambling game—and this way to express probability might be the most useful way of all:

Expressing Probabilities in Odds Format

In casual conversation, the word “odds” is often used as a synonym for probability.

This is correct as far as that goes, but it has a more specific meaning:

It’s a way of expressing a probability in terms of the ways something can’t happen versus the ways it can happen.

The odds of getting a total of 2 when rolling a pair of dice are 35 to 1.

There are 35 ways of rolling something other than 2.

And there’s one way to roll a 2.

Why is this more useful than the other means of expressing probability?

That’s simple—because you can look at the odds offered by the payout for a bet to determine how good or bad a bet is.

Casinos, by the way, almost never offer a bet that fair. They want to pay you off at odds that are lower than your odds of winning. The difference between the payout odds and the odds of winning constitute the house edge, which is where the casino makes its profit.

In fact, you can place a bet with the casino that the next roll of the dice will result in a 2. And if you win, you’ll get 30 to 1 on your money.

See the discrepancy there?

That’s where the casino makes its money.

You can translate that into an average percentage of each bet lost to get the house edge fairly easily, too. Just assume that you make 36 bets at $100 each. You also assume that you’ll have a statistically perfect set of results, meaning you’ll win once and lose 35 times.

You’ll lose $3500 total, but on the one roll you win, you’ll win $3000. Your net loss is $500.

Since you made 36 spins, your average loss per spin is $500/36 spins, or $13.89.

Since $13.89 is 13.89% of $100, we say that the house edge on that bet is 13.89%,

That’s a high house edge, by the way. Most table games in the casino offer bets that have a house edge of 5% or less—much less in many cases.

This is true of the various craps bets, too. I intentionally showed you the probability and the house edge for one of the worst bets at the craps table.

Another possible bet is a bet on “any 7.” This seems like it might be a lot better of a bet, because you’re a lot more likely to win this one.

Since you have a probability of 6/36, you can reduce that just like any fraction, to 1/6. This converts to 5 to 1 odds on that bet.
If you win this bet, you get paid off at 4 to 1 odds.

But even though you’ll win this bet a lot more often than the bet on “snake-eyes,” it’s actually a much worse bet.

Let’s do the same math. $100 per bet, this time on 6 bets, and you lose 5 times, winning once.

That’s $500 in losses and a $400 win, for a $100 net loss.
$100 in losses over 6 spins averages out to $16.67 lost per average on each bet.

That’s a whopping house edge of 16.67% on the “any 7” bet.

Wait a Minute! Didn’t You Say that Craps Was One of the Better Bets in the Casino?

Craps does indeed offer some of the best odds in the casino. You just need to stay away from the bad bets, of which there are plenty.

Here’s what you need to know about that craps table that I said wasn’t as important as you might think:

Now it’s time to talk a little bit about how the game works:
Craps requires someone to roll the dice—a shooter. The role of shooter rotates around the table. The shooter’s goal is to “succeed.”

Here’s how the shooter succeeds:

• If he rolls a 7 or 11, he’s rolled a natural. That’s an automatic success.
• If he rolls a 2, 3, or 12, he’s rolled “craps.” That’s an automatic failure.
• If he rolls any other total, he’s “set a point.” He continues to roll until he rolls a point or rolls a 7. If he rolls the point again, he succeeds. If he rolls a 7 before rolling the point again, he fails.
• You (and the shooter, by the way) can choose to bet on his success or failure. These bets are 2 of the best bets at the craps table.
• If you’re betting on the shooter to succeed, you’re placing a pass line bet.
• If you’re betting on the shooter to fail, you’re placing a don’t pass bet.
• The house edge on these 2 bets is 1.41% and 1.36%. The don’t pass bet offers slightly better odds.

Most players are willing to give up the 0.05% out of a sense of camaraderie. It’s just more fun to root for someone during a game than it is to root against them.

In fact, someone who bets the pass line is called a “right bettor.” Someone who bets the don’t pass line is called a “wrong bettor.”

But there’s really nothing wrong with either bet. Nick the Greek was famous for being a wrong bettor, in fact.

The Odds Bet in Craps Might Be the Best Bet in the Casino

There are only 2 bets in the casino which have a house edge of 0%. The first of these is the double-up bet on some video poker games. They give you a 50% chance of doubling your winnings.

The other is the odds bet in craps.

And it’s not even labeled on the craps table!

The odds bet is a bet you can make after a point has been set. (You can’t place this bet otherwise.)

It pays off if the shooter rolls the point before rolling a 7.

But what’s great about this bet is that it pays off at the same odds as you have of winning. The payoff odds are based on what the point is, as follows:

• If the point is 4 or 10, the odds bet pays off at 2 to 1.
• If the point is 5 or 9, the odds bet pays off at 3 to 2.
• If the point is 6 or 8, the odds bet pays off at 6 to 5.

Those are the exact same odds as the odds of winning are, so you’re able to place a bet with no house edge.

Of course, if you bet the don’t pass line, you can still take the odds bet, but the payoff odds are reversed. You get paid if the shooter rolls a 7 before rolling the point.

In either case, when you put the extra money into action, you’re effectively reducing the house edge on the total amount of money you have on the table.

The more you bet on the odds, the lower your cumulative house edge becomes.

Of course, casinos usually limit the amount of money you can place on the odds bet. It can vary widely, but it’s always better for the player to be able to bet more on the odds bet rather than less.

By the way, to place the odds bet, you put the chips behind your original pass or don’t pass wager.

The Come and Don’t Come Bets

The pass line and don’t pass bets aren’t the only 2 basic bets at the craps table. Once a point has been established, you can place a bet on the next roll that treats it as if it were a new come out roll.

These bets are called the come and don’t come bets, and they work exactly like the pass line and don’t pass bets. You can even place an odds bet after them.

These should also be part of your arsenal.

The Perfect Craps Strategy

Now all you need to do is avoid all the lousy bets at the table and stick with the good bets. That’s the perfect craps strategy.

Don’t worry about betting systems. Don’t try to hedge your bets. Don’t spend a bunch of money on instructional videos that are going to teach you how to control or influence the results of the dice.

You don’t need any of that stuff to enjoy some of the best odds in the casino.

Conclusion

Craps in the casino can be intimidating because of the table and all the bets that are available on it. But don’t forget that people have played craps on the streets with no fancy table for decades.

Craps is a simple game with simple probabilities. It also offers some of the most fun in the casino, along with some of the best odds. All you need to do to take advantage of these great odds is stick with the easy bets at the table:

• Pass and don’t pass
• Come and don’t come
• Odds

All the other bets at the craps table are sucker bets.

Now that you know this, you don’t have to be a sucker.